Colorblind simulation model testing revisted

Addendum added May 7, 2017

Changes to my Colorblind Simulation Pro app necessitated an update to the original article "Are colorblind simulation models accurate?". The changes that altered the test results are as follows:

1. The lack of documentation for the Linear simulation model resulted in its replacement with the ImageJ plugin.
2. In the initial study, data collection was a manual process. The Colorblind Simulation Pro app now includes an activity that automatically executes and scores the Farnsworth D-15 Dichromatic Panel test.
3. The automated cap order is sorted to match how humans sort colors, instead of the manual hue based sort.
4. The test scores now include the TCDS (Total Color Difference Score).

Once again, the tests show that visually evaluating an image does not prove that a model is accurate. The output of a simulation should produce results that correspond to human perception. It is not the color produced that is important, it is accurate simulation of the confusion produced by the type of CVD.

CVD simulation models tested

The CVD simulations models tested are those present in version 1.1.4 build 36 of the Colorblind Simulation Pro. All simulation models have the following characteristics:

• The original source code for all models is available on the Internet. They all have an open source license. I preserved the routines that perform the simulation calculations. The UX routines were changed to fit the Android framework.
• The authors of the original source code designed the simulation models to use the sRGB color space. The sRGB color space is the default color space for Web browsers and mobile devices. Since Android lacks color management, the tests were limited to the sRGB color space.

The models tested are as follows:

• Meyer-Greenberg-Wolfmaier-Wickline (MGWW)
  The first computer simulation work was done in 1988 by Gary W. Meyer and Donald P. Greenberg. Thomas Wolfmaier wrote a Java applet around 1999 that used Meyer and Greenberg study to create a CVD simulator. Two years later Matthew Wickline published his improved version of Wolfmaier's code. The MGWW model converts sRGB colors to the CIE XYZ color space. MGWW does not transform CIE XYZ to CIE LMS.
• Brettel-Vienot-Mollon (BVM)
  In 1997, Hans Brettel, Francoise Vienot and John D. Mollon published Computerized simulation of color appearance for dichromats. BVM converts sRGB values directly to the CIE LMS color space, instead of following the two step process of converting to CIE XYZ and then to CIE LMS. The authors of the study do not mention which Chromatic Appearance Model (CAM) was used to perform the transformation to the CIE LMS color space. The source code code used in the Colorblind Simulation Pro app is based on the Gimp source code.
• Machado-Oliveira-Fernandes (MOF)
  While MGWW and BVM focused on dichromats, Mechado-Oliveira-Fernandez sought to create a simulation model for both dichromats and anomalous trichromats. Where MGWW and BVM follow the Young-Helmholtz theory of color vision, MOF follow the stages theory. The stages theory, or zone theory, holds that the Young-Helmholtz theory works at the photoreceptor level, but signals are then processed according to Hering's component theory. The only source code available is the pre-calculated tables provided in the above article.
• ImageJ CVD Plugin (ImageJ)
  The ImageJ CVD plugin is a version of MGWW that uses pre-calculated tables. The author of the code does not provide any details as to the process for determining the pre-calculated values. This ImageJ plugin is similar to the Vischeck plugin.

Test environment

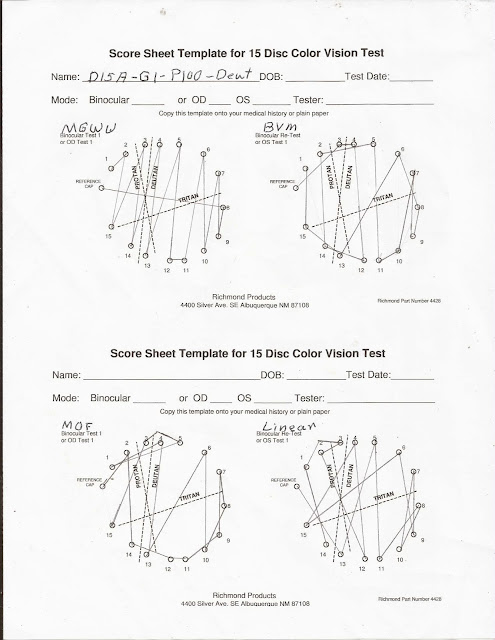
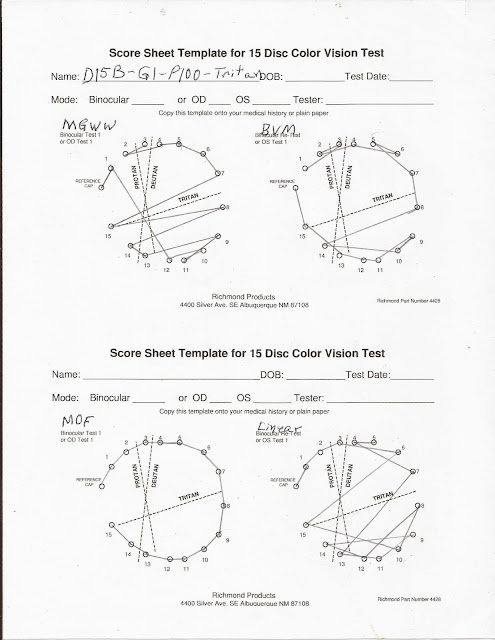
The automated version of the Farnsworth D-15 Dichromatic Panel test produces more accurate results and provides more information. The test activity uses both the Colblindor (D15A) and Color Blindness (D15B) sRGB values for the 16 caps (Pilot cap + 15 caps).  The following images show the output of the D-15 activity for the Colblindor RGB colors. The test conditions are for deuteranopia with a gamma of 1.0 and 100% colorblindness. The first screenshot is for a person with normal vision. This screenshot is followed by images for the MGWW and BVM models.

Figure 1 - D15A Normal color vision

Figure 2 - D15A Deutan MGWW

Figure 3 - D15A Deutan BVM

The order of the caps was determined as follows:

1. The sorting algorithm used is a modified version of the Traveling Salesman Problem. The algorithm produces a minimum TCDS, by using the CIE L*A*B* color distance.
2. Although it is rare, the cap order for duplicate RGB values is in ascending order.

Simulation of the Farnsworth D-15 test is available in Colorblind Simulator Pro version 1.1.4 build 36, and newer. This is strictly a beta activity, and is available under the options menu.

Since Colblindor and Color Blindness use different RGB values for the caps, there are variations in the output.

Scoring tests

The scoring of the tests is impacted by the following:

1. The Munsell colors selected by Farnsworth have different hue values, while holding the saturation and value to a constant value of 6. Neither set of RGB values hold the initial values for saturation and brightness to a constant value. Consequently, the RGB version of the test introduces variables that were not part of the original test design.
2. The RGB colors are constrained to the sRGB color space. Some of the Farnsworth D-15 Munsell color codes fall outside of the sRGB gamut of colors.

The traditional scoring sheets provide a visual means of showing the deviations from a normal color wheel. The cap order in Figures 1 thru 3 depict a normal and two deuteranopia color wheels. The article Color Perception by Michael Kalloniatis and Charles Luu provides samples of the human response to the Farnsworth D-15 Panel. Figure 4 shows the graphs that are relevant to this article.

Figure 4 - Sample human response to D-15 panel

The dashed lines for PROTAN, DEUTAN and TRITAN are used to score the test. The transitions that are parallel to a line count as an indication of that form of CVD. Minor transitions, such as a cap order of 2, 4, 3, 5, are consider as normal.

The article "A Quantitative Scoring Technique for Panel Tests of Color Vision" by Algis J. Vingrys and P. Ewen King-Smith defines another method for scoring the Farnsworth hue tests. I converted the BASIC code in the article to the Java code used in the automated tests. I added the code required to generate the TCDS, using the same approach as Bowman's Munsell color distances. The following provides a brief guide for interpreting the output:

• Angle
  The confusion angle identifies the type of color deficiency. According to Vingrys and King-Smith, an angle between +3.0 and +17.0 indicates protanopia, deuteranopia angles range between -4.0 and -11, while tritans have an angle greater than -70. Colblindor expands the ranges: protan defect begins at +0.7, from +0.7 to -65 is a Deutan defect, and less than -65 is a tritan defect.
• Major and minor radius
  Vingrys and King-Smith use the moments of inertia method to determine color difference vectors. The major and minor moments of inertia are converted to major and minor radii to preserve the same unit of measure as used for the angles. These values can be used to determine the severity of the defect.
• Total Error Score (TES)
  In math terms, TES is the root mean square of the sum of the major and minor radii. Scores have an approximate range of 11 to 40+, with higher values indicating greater severity.
• Total Color Difference Score (TCDS)
  The book "Borish's Clinical Refraction" by William J. Benjamin provides the color difference tables used by K.J. Bowman (A method for quantitative scoring of the Farnsworth panel D-15. Acta Ophthalmologica. 1982, 60:907-915). However, these tables are based on color differences for the Munsell color codes. RGB color differences do not reflect human perception. Consequently, I use CIE L*A*B* for calculating color differences. Since quantitative scoring is based on normal color values, the sRGB TCDS is also based on normal sRGB values, and not the simulated values.
• Selectivity Index (S-Index)
  The S-Index is the ratio of the major and minor radii. Values less than 1.8 indicate normal vision, or random values.
• Vingrys' Confusion Index (C-Index (V))
  Vingrys' C-Index is the major radius of the subject divided by the major radius for normal vision. The dividing line between normal and defective is 1.60.
• Bowman's Confusion Index (C-Index (B))
  Bowman's C-Index is the TCDS of the subject divided by the normal TCDS. The color differences are based on CIE L*a*b* color distances, not the Bowman color distance table.

Test results

Tests were run for protanopia, deuteranopia, and tritanopia (100% CVD) for the following conditions:

1. Each test was run with a gamma of 1.0 and 1.2 to determine if gamma impacted on the test results. Since the system gamma is 1.0, these values reflect the adjust to the system gamma. The effective display gamma is 2.0 and 2.2. Gamma adjustments greater than 1.5 tend to shift the colors such that there is a large increase in colors that are outside of the sRGB gamut. For compatibility with older terminals, the default gamma for sRGB is 2.2.
2. Tests were run for both the Colblindor (D15A) and Color Blindness (D15B) RGB values for the Farnsworth D-15 Dichromatic panel.
3. All four models were tested.

The results are presented according to the type of CVD. The graphical score sheets are presented first. The analytical test scores are shown next, followed by a discussion of the raw data.

Protanopia

The following score sheets are for a gamma of 1.0.

Figure 5 - D15A Gamma 1.0 Protanopia

Figure 6 - D15B Gamma 1.0 Protanopia

The gamma 1.2 score sheets are as follows:

Figure 7 - D15A Gamma 1.2 Protanopia

Figure 8 - D15B Gamma 1.2 Protanopia

The quantitative scores for protanopia are shown in Figure 9.

Figure 9 - D15 Quantitative Scores for Protanopia

Summary of protanopia test results for each simulation model:

• MGWW
  The MGWW model returns the same cap order for all tests. Although it has fewer lines parallel to the protan line, the cap order is similar to that shown for protanopia in Figure 4. All the test scores for MGWW indicate protanopia. With a few variations, the cap order matches the hue order.
• BVM
  BVM results vary from protanopia to deuteranopia depending on the test conditions. The protanopia results are limited to D15B. For D15A, the results are for protanomaly or deuteranomaly. Figure 7 shows a very unusual confusion diagram in which caps 4 and 5 are reversed.
• MOF
  MOF returns the same results of MGWW. However, the colors generated are radically different. Unlike MGWW, there is no apparent relationship between the hue and the cap order.
• ImageJ Plugin
  With a gamma of 1.0, the ImageJ plugin matches MGWW for both D15A and D15B. With a gamma of 1.2, the results are slightly weaker, but still in the protanopia range.

Deuteranopia

The following score sheets are for a gamma of 1.0.

Figure 10 - D15A Gamma 1.0 Deuteranopia

Figure 11 - D15B Gamma 1.0 Deuteranopia

The gamma 1.2 score sheets are as follows:

Figure 12 - D15A Gamma 1.2 Deuteranopia

Figure 13 - D15B Gamma 1.2 Deuteranopia

The quantitative scores for deuteranopia are shown in Figure 14.

Figure 14 - Quantitative Scores for Deuteranopia

The following summarizes the test results for deuteranopia:

• MGWW
  For MGWW, the D15A cap order is the same for a gamma of 1.0 or 1.2. Although slightly different than the D15A cap order, the D15B cap order also is not gamma dependent. For both D15A and D15B, the cap order is a reasonable variation of the cap order shown in Figure 4. The angles for D15A and D15B (see Figure 14) are both in the deuteranopia range.
• BVM
  BVM is not sensitive to gamma, but it provides different results for D15A and D15B. Figure 10 shows a very unusual confusion diagram in which caps 4 and 5 are reversed.
• MOF
  MOF mimics MGWW, but with different colors. 
• ImageJ Plugin
  The test results show that the ImageJ plugin is gamma sensitive for D15A, but not for D15B. The ImageJ plugin does produce different results for D15A and D15B. Although it is based on MGWW, the results are not the same.

Tritanopia

The following score sheets are for a gamma of 1.0.

Figure 15 - D15A Gamma 1.0 Tritanopia

Figure 16 - D15B Gamma 1.0 Tritanopia

The gamma 1.2 score sheets are as follows:

Figure 17 - D15A Gamma 1.2 Tritanopia

Figure 18 - D15B Gamma 1.2 Tritanopia

The quantitative scores for tritanopia are shown in Figure 19.

Figure 19 - D15 Quantitative Scores for Tritanopia

The following summarizes the test results for tritanopia:

• MGWW
  For a gamma of 1.0, MGWW reports the same values for D15A and D15B. However, MGWW is gamma sensitive with different values for a gamma of 1.2. While there are variations in the results, all tests reflect tritanopia.
• BVM
  For tritanopia, BVM is not gamma sensitive. BVM reports the same results for both D15A and D15B. The results match those of MGWW with a gamma of 1.0, although the colors are different.
• MOF
  As shown in 15 through 18, MOF has an unusual pattern that lowers its score in Figure 19.
• ImageJ Plugin
  For D15A, the ImageJ plugin is gamma sensitive. However, it is not gamma sensitive for D15B. For D15B with a gamma of 1.0, the results reflect tritanomally and not tritanopia.

Analysis of test results

This test of simulation models was limited to four questions. The answers to these questions raise further questions that become the subject of future tests.

Do the RGB colors alter the test results?

As mentioned above, there are two sets of RGB colors used for the Web version of the D15 Panel: Colblindor (D15A) and Color Blindness (D15B). For the deuteranopia, every model produced different results for D15A and D15B. For protanopia, only BVM produced different results. MGWW and the Image plugin produced different results with tritanopia.

Again, the differences are in regards to color confusion. For BVM and the ImageJ plugin, the differences in confusion changed the diagnosis.

Does gamma make a difference?

For all forms of CVD, the ImageJ plugin resulted in different confusion diagrams. For protanopia, BVM showed major changes between gamma 1.0 and 1.2, which actually altered the diagnosis. MGWW exhibited differences in confusion for tritanopia, but the results did not alter the diagnosis.

Which model returns the best results?

Using color distance as a metric for ordering colors made a tremendous difference in test results. The results are surprising.

Even though it uses pre-calculated tables, MOF (Machado-Oliveira-Fernandes) produced the most consistent results, with no significant failures. MOF is also the only model based on the stages theory of color vision and the theory that replacement cones have shifted frequencies.

BVM (Brettel-Vienot-Mollon) had a problem differentiating between between protanopia and deuteranopia for the protanopia tests. Of the four protanopia test cases, BVM only returned the correct result for D15B with a gamma of 1.0.

MGWW never returned a bad result, but did create different results depending on RGB colors and gamma. Although based on MGWW, the ImageJ plugin tended to produce different results. These results were sensitive to both the gamma and the RGB color set.

Based on the current test results, I would rank the results from best to worst as MOF, MGWW, ImageJ plugin, BVM.

Do the simulations models mimic human response

The article by Vingrys and King-Smith includes a table of human responses to the Farnsworth-Munsell D-15 panel. Following is a partial replica of that table:

Figure 20 - Vingrys & King-Smith Test Results

I replaced the TCDS data in the Vingrys and King-Smith paper, with values based on Bowman's color distance table. The data now matches the calculations from  www.torok.info/colorvision/dir_for_use.htm.

The normal values match those generated by the D15 test simulator (see Figures 9, 14 and 19). This verifies that the algorithms used are correct. If the algorithms are correct, why are simulated scores not similar to the human scores? This is especially true for protanopia and deuteranopia. Except for the ImageJ plugin, the tritanopia simulation scores are reasonably close to the human scores.

Perhaps, the key to answering this question lies in the difference color distances. The following table show the Bowman color distances for the Munsell colors. The D15A and D15B color distances are based on the CIE L*A*B* color distances.

Figure 21 - Color distances from pilot cap

Figure 21 shows just one row of the the entire table. Providing a complete table that matches Bowman's table is a future task. It should be noted that the greater the color distance, the easier it is to separate two colors.

Conclusions

These tests highlighted several issues:

• The different results between D15A and D15B raises questions about the RGB colors used in digital testing on the Web and mobile devices. There is a possibility that the Munsell colors used in the Farnsworth D15 test are outside the sRGB gamut of colors. If this is the case, the solution is a color corrected device with color management software. This would allow the use of other color spaces, such as Adobe RGB.
• Color correction will not solve the color distance problem. For the Web based tests to match the physical test, the RGB color distances must closely  match the Munsell color distances.
• No model produces results that matched those in Figures 4 or 18. Whether this reflects a problem that is inherent in the models is difficult to determine. Resolution of the first two issues should help answer this question.

The results produced by these tests are educational, in that they:

• Emphasis that each person has a color wheel. Both the FM 100 and D15 tests are color wheels.
• CVD is not just a rotation of the color wheel, color confusion changes the order of the colors.
• Simulation of CVD is about color confusion. We do not know the colors seen by any person.

The following images are for each of the models tested with a gamma of 1.0. Each image is a concatenation of the normal, protan, deutan, and tritan images.

Figure 22 - MOF

Figure 23 - MGWW 

Figure 24 - ImageJ plugin

Figure 25 - BVM

What do these images tell us about the validity of each model?

Nothing!

Images emphasis color, which is an illusion.

Images hide the transitions that cause confusion.

Images are useless when selecting text colors.

Addendum

Additional research impacts on the analysis of the results of the above tests. After months of searching for a list of the Munsell color codes for the Farnsworth D15 Dichromatic Panel test, I found the list in a 1947 edition of the manual, in Japanese. With the help of EasyRGB, I was able to construct the following color distance table:

Figure 26 - Munsell Delta E Table

From Figure 26, we can see that the color distances for D15A reflect a significant departure from the Munsell colors. D15B is much closer to the actual Munsell colors. However, D15A and D15B have a bigger problem.

The Munsell color codes  are Hue Value (luminosity) / Chroma (roughly equivalent to saturation). From Figure 25, we see that the hue changes, while the luminosity and chroma remain constant (except for the chroma of the Pilot cap). When converted to CIE XYZ, luminosity is represented by the 'Y'. For CIE L*a*b*, the 'L' is the luminosity. These CIE color spaces do not have a specific field for chroma.

Figure 27 shows the work sheet for D15A, while Figure 28 shows the work sheet for D15B. Note that neither D15A nor D15B maintain a constant luminosity for all caps. Furthermore, the nearest Munsell color for the cap RGB value, does not match the Munsell colors in Figure 26. Except for cap 11, D15B colors correlate to the same Munsell colors as in Figure 26. The Delta E column is the color distance of the RGB value from the color in the Munsell column.

Figure 27 - D15A Munsell Worksheet

Figure 28 - D15B Munsell Worksheet

For comparison, Figure 29 shows the worksheet for EasyRGB color conversion from Munsell to sRGB. I have other Munsell conversion worksheets, but chose this one to avoid explaining the conversion from Illuminant C to D65. Munsell color are usually expressed using Illuminant C (average daylight), while sRGB normally uses D65 (high noon).

Figure 29 - EasyRGB Munsell Worksheet

Yes, the EasyRGB values due make a difference on the Farnsworth D15 test results for the colorblind simulators. While there is much work yet to be done, the goal of being able to test different models for colorblind simulation is getting closer to completion.

One RGB model, many RGB spaces

The RGB (Red, Green, Blue) color model dates back to 1860 and the Young-Helmholtz trichromatic theory of color vision. In fact, all color models are tied to human color vision. Color models that define a light source, such as RGB, are additive. Color models for paints and objects, such as CMYK, are subtractive. Additive color models combine colors. Subtractive color models define the color refracted when a photon of light strikes a surface.

The RGB color model does not provide a colorimetric definition of red, green, and blue. The model defines colors in reference to the primary colors.

Figure 1 - RGB Color Model
(credit: Wikipedia)

RGB specifies a color by defining its location within a three dimensional matrix. Each index has a value that is between 0 and 255. This provides for a maximum of 16,777,216 possible colors. However, humans with normal color vision can only detect around ten million colors.

Human color perception is based on the response of the three cone types to a photon of light. Each of the cone types have their own frequency response curve for responding to photons, as shown in Figure 2.

Figure 2 - Human cone response

RGB color space

With the specification of the chromaticity of red, green and blue, the color model becomes a color space. Chromaticity defines the quality of a color, without referring to luminescence. The two parameters for chromaticity are hue and chroma (also called saturation, intensity).

To define the boundaries of the RGB color space, we need to know the chromaticity for three points: red (1,0,0), green (0,1,0) and blue (0,0,1). The problem is that the RGB model lacks definitions for chromaticity or luminosity.  For a solution to this problem, we need to look at the color spaces defined in 1931, by the International Commission on Illumination (CIE). The 1931 CIE color spaces define the quantitative link between the wavelength of light and the human perception of color. The CIE 1931 color spaces are foundation on which modern color spaces are built. They are also important to understanding the mechanics behind colorblind simulation. For the purpose of this article, the important CIE color spaces are described below.

CIE XYZ color space

The CIE XYZ color space is a device independent color space that represents all the color sensations experienced by an average person, as shown in Figure 3. It serves as a standard reference for other color spaces.

Figure 3 - CIE XYZ color space (colors displayed are limited to sRGB color space)
(credit: Wikipedia)

Figure 3 is actually a chromaticity diagram that compresses the three dimensional color space for the three different cone types into two dimensions. The enclosed space represents the gamut of human colors. The curved edge of the diagram shows the light frequency in nanometers. The straight edge is known as the line of purples (colors for which there is no single monochromatic source).

CIE RGB color space

Unlike the CIE XYZ color space, the CIE RGB color space defines a the color space resulting from the mixing of three monochromatic light sources. It was the first color space to be based on adding three primary colors. Figure 4 illustrates the gamut for the CIE RGB color space.

Figure 4 - CIE RGB color space
(credit: Wikipedia)

The triangle in Figure 4 defines the gamut for the CIE RGB color space. The circle with the label "E" is the white point. Since computers did not exist in 1931, this color space served as a reference study for color vision research.

CIE L*A*B* (CIELAB) color space

It is important to keep in mind that this entire discussion revolves around human color vision. The Young-Helmholtz trichromatic theory is not the only color vision theory. In the late 19th century, Ewald Hering developed the opponent-process theory of color vision. The opponent-process theory holds that the cone photoreceptors combine to form three opposing color pairs: blue/yellow, red/green/, and black/white. The opponent-process theory explains human color experience, such as why we don't see "bluish yellow" or "reddish green". It all helps explain why individuals who are dichromatic confuse either red and green or blue and yellow. The stages theory of color vision holds that the trichromatic theory functions at the photoreceptor level, while the opponent-process theory functions at the neural level.

In 1976, CIE released the CIE L*A*B* color space, which is based on the opponent-process theory of color vision. The vertical axis represents lightness (L*), with values ranging from 0 (black) to 100 (white). The range of the values for a* and b* are usually from +100 to -100 or +127 to -128. Figure 5 illustrates the CIELAB color space (note: there is a label error in the diagram, as Blue should be -b).

Figure 5 - CIE L*A*B* color space
(credit: Wikipedia)

The CIELAB color space is device independent, and incorporates the entire gamut of human perceivable  colors. The CIELAB gamut does include colors that are outside the human gamut. Since it does incorporate the entire human gamut of colors, CIELAB is often used to convert colors from one color space to another.

Device dependent color spaces

The above color spaces were all device independent. In regards to device dependent color spaces, this article only covers the most popular of the current digital RGB color spaces. Besides the chromaticity of the three primary colors, a color space requires a white point. A white point is that point where the chromaticity coordinates produce the color white. The two most common illuminants used to define a white point are D50 (horizon light) and D65(noon daylight).

Figure 6 - Color space comparisons
(credit: Wikipedia)

 Figure 6 compares the most common color spaces in use. Except for SWOP CMYK (a typical printer color space), the color spaces are all RGB. Every RGB color space shown in Figure 6 uses the same range of values to address colors. For example, the color code red=120, green=154, blue=48 references a different color in each color space. The CIELAB color space acts an intermediary color space for color space conversion.

sRGB color space

Created by Microsoft in 1998, sRGB has the smallest gamut of all the color spaces. sRGB acts as the least common denominator. In Web design, CSS uses sRGB. The common format across all Web browsers is sRGB. As of this writing, Android and iOS only support sRGB (iOS 10 also supports DCI-P3 on the iPad Pro 9.7").

Adobe RGB

With its larger color gamut, Adobe RGB is probably the most popular color space for working with images. For mobile devices and Websites, Adobe RGB images must be converted to sRGB. 

Without conversion to sRGB, Adobe RGB images are darker and muted.

Colormatch RGB

This color space was originally designed for the PressView line of calibrated displays. The gamut for Colormatch  is only slightly larger than sRGB in the blue-green region, but a smaller gamut in the red-blue region.

ProPhoto RGB

Eastman Kodak designed the ProPhoto (ROMM) color space as a RGB color space for editing images. The ProPhoto primaries are not linked to any monitor specification. The large gamut minimizes the loss of color. However, the ProPhoto gamut does have out-of-gamut colors for human vision. ProPhoto uses the D50 white point, and not D65.

Color profiles versus color spaces

A color profile is an implementation of a color space. According to the International Color Consortium (ICC - CIE in French), profiles define the color attributes for a particular device or viewing requirement via a map between the device or color space and a profile connection space (PCS). The PCS is either CIE L*A*B* or CIE XYZ. Mappings can be specified using either tables or a series of transformation parameters.

 When a color profile is embedded in a file, the file is said to be tagged. Color management is the controlled conversion between color spaces. Lacking color management, sRGB is the default color space. Web browsers do not support color management. Thus, sRGB is the default color space.

Android does not support color management. However, Samsung's "Screen mode" performs color management. The options vary depending on the whether the device has an AMOLED screen, and the Android version. For AMOLED devices:

•  "Basic" or "Standard" is sRGB without modifications.
•  The "Adaptive display" mode boosts the brightness for viewing screen in daylight, and only applies to a few applications.
•   The "Photo" or "Professional photo" seems to support Adobe RGB, as it has a much larger gamut.
• The "Cinema" mode appears to support a gamut similar to DCI-P3.

For reasonable consistency across all devices and Web browsers, the sRGB color space is still the only common denominator. Without color management, an device automatically displays images in all color spaces as if they used the sRGB color space.

Conclusion

Not only is color an illusion, color consistency across all devices is illusive. Even an sRGB image will appear differently on different devices. Not only are there hardware variations, variations in screen brightness and surrounding light change the appearance of colors. The only solution is to color calibrate every display device. Color spectrometers are rather expensive, so the only other choice is to accept that a certain degree of color variation across devices is a reality. 

Are colorblind simulation models accurate?

This article has been replaced with

http://colorblindtools.blogspot.com/2017/02/colorblind-simulation-model-testing.html

Accurate in what sense? The colors produced in an image do not determine accuracy, for we know that color is an illusion. What counts is the ability to discriminate between different shades of color. We do not know the color a person actually sees, but we do know that protans and deutans confuse shades of red and green. Consequently, the color generated by a colorblind simulator is not important. What is important is that the simulated color reflects the same confusion as experienced by an individual with Color Vision Deficiency (CVD).

Test Environment

Selecting a color blindness test was the first challenge. My goal was to use a test that could be automated. While it is a common test, the Ishihara Test Plates do not meet this criteria, and are only used for initial screening. The Farnsworth-Munsell 100 Hue (FM-100) test meets the criteria, as does the Farnsworth Dichotomous (D-15 Panel) test. For the initial round of testing, I used the D-15 Panel, with a minimal amount of coding and a lot of manual data collection.

The FM-100 and D-15 Panel test are classed as hue discrimination, or arrangement, tests. As the name implies, these tests use the Munsell color system. The Munsell color system is a three-dimensional system based on hue, chroma, and value. On the other hand, the RGB color system has no sense of chromaticity or luminosity. There is no nice one-to-one conversion between Munsell and RGB. Yet, there are computer based tests for the FM-100 and D-15 panel tests that use the RGB color system.

Both Colblindor and ColorMunki provide Web versions of the FM-100 Hue test. Both sites use the same RGB colors for the each of the four panels. Daniel Flück of Colbindor created the original on-line version of the D-15 Panel test. Color Blindness also offers this test, but the RGB colors are different. In my tests, the Colbindor version is referred to as D15A, and the Color Blindness version is D15B. The two versions produce different results.

Since the Farnsworth tests are all based on the hue of a color, the RGB colors were converted to HSV to obtain the hue. The Munsell colors used by Farnsworth have a chroma equal to 6 and a value equal to 6. The only variable is the hue. When the RGB colors are converted to HSV the values for saturation and value are not constant. The same holds true for saturation and luminosity under the HSL color system.

The FM-100 hues for normal vision are correctly spaced and form a color wheel. While the hue values were different, the normal vision hues for both versions of the D-15 test were OK. Under the Munsell color system, the hue is a integer value between 1 and 360. With HSV, or HSL, it is a float value such that the hue >= 0 and <= 359. Rounding the float value to an integer produced too many duplicate simulation values. Changing the float to ###.## greatly reduced the duplication problem. There are still cases where a model generates the same RGB value for two caps, or the same hue for different RGB values. The hue values were generated by a Quick Test feature that is only enabled in the debug mode of my Colorblind Simulator Pro app.

Scoring the tests

I initially scored each test using the traditional scoring sheets from Richmond Products. While these score sheets were designed for binocular vision tests with a retest, they work perfectly for scoring and comparing the four models that were the subjects of my tests. When compared with the quantitative results, the graphic drawings provide additional clues into the behavior of a model.

The article "A Quantitative Scoring Technique for Panel Tests of Color Vision" by Algis J. Vingrys and P. Ewen King-Smith includes the source for a scoring program. This program forms the basis for the scoring of the on-line tests described above. While Daniel Flück created a JavaScript version of the PC BASIC program, I created a Java version.

The tables in the article by Vingrys and King-Smith include a column for TCDS (Total Color Difference Score). The calculation of this score is not part of the BASIC program included in the article. Although the book "Borish's Clinical Refraction" by William J. Benjamin provides the color difference tables used by Bowman, the calculation of TCDS is still a problem for the following reasons:

1. The cap differences are based on the Munsell colors. For example, the Munsell color difference (Delta-E) between the Pilot cap and Cap 1 is 9.4. For the RGB color system, the Delta-E for Colblindor (D15A) is  9.491 and 8.8034 for Color Blindness (D15B). The differences in Delta-E values could have an impact on the ability to distinguish colors.
2. Using the Bowman tables described in Benjamin's book, the TCDS for normal vision is 117. However, Vingrys and King-Smith show a normal vision TCDS of 165, with no explanation of the difference with Bowman. Without a formula for calculating TCDS, comparative analysis is not possible.

Simulator models tested

All tests are limited to the four models that are part of my Colorblind Simulator Pro app, debug version 1.1.1 build 23. The Quick Test activity of the debug version includes additional output that is not part of the released version. This output was designed for model testing. A modified version of this feature may appear in a future release.

Meyer-Greenberg-Wolfmaier-Wickline (MGWW)

The first computer simulation work was done in 1988 by Gary W. Meyer and Donald P. Greenberg. The goal of their study was to create a digital means of administering the Farnsworth-Munsell 100 Hue test. Anyone wishing to have a better understanding of the FM-100 test should read this article.

The study by Meyer and Greenberg:

• Converts RGB to CIE XYZ color space
• Adjustments were made to keep output RGB values within the range of 0 to 255.

While the Meyer and Greenberg study was published in 1988, Thomas Wolfmaier wrote a Java applet around 1999 that used their study to create a CVD simulator. Two years later Matthew Wickline published his improved version of Wolfmaier's code. Thus, this model is referred to as MGWW. The Colorblind Simulator Pro app implements Wickline's code.

Brettel-Vienot-Mollon (BVM)

In 1997, Hans Brettel, Francoise Vienot and John D. Mollon published Computerized simulation of color appearance for dichromats. Even though it was published 11 years earlier, Brettel-Vienot-Mollon do not reference the work of Meyer-Greenberg. The differences between BVM and MGWW are:

• BVM converts RGB to LMS and not CIE XYZ
• The BVM algorithm makes no attempt to limit out-of-bound conditions for RGB values
• The goal of BVM was to build a simulator for images
• Based on reports by unilateral dichromats (one normal eye and one dichromatic eye)

Machado-Oliveira-Fernandes (MOF)

While MGWW and BVM focused on dichromats, Mechado-Oliveira-Fernandez sought to create a simulation model for both dichromats and anomalous trichromats. Where MGWW and BVM follow the Young-Helmholtz theory of color vision, MOF follow the stage theory. The stage theory, or zone theory, holds that the Young-Helmholtz theory works at the photo-receptor level, but signals are then processed according to Hering's component theory.

For anomalous trichromacy, MOF theorize that the degree of deficiency depends on the amount of shift in the cone wavelength sensitivity. For dichromacy, the deficient cones are replaced by cones with another frequency range.

MOF created a C++ version of the FM100 test to verify their theory. Their test group consisted of 17 male subjects with normal vision and 13 male subjects with protanopia, protanomaly, deuteranopia or deuteranomaly. The test group did not include any tritans.

The only source code available is the precalculated tables provided in the above article. The lack of complete source code makes it difficult to reproduce their test results.

Linear 

The linear model is a precalculated version of the BVM model. Loren Petrich provides the model in his source code, with no references as to its origin. Sometimes the output matches the output from BVM, and other times it is radically different.

Test results

All tests were scored using both the 15 Disc Color Vision Test score sheets, and the quantitative methods of Vingrys and King- Smith. Besides the Vingrys and King-Smith article, the Farnsworth and Lanthony Test Instructions provides illustrations for interpreting the charts. The following table provides a baseline for interpreting Vingrys and King-Smith scores.

Table 1 - Results of vector analysis

Type of Cap Arrangement	Angle	Major Radius	Minor Radius	TES	S-Index	C-Index
Normals:
No error	62.0	9.2	6.7	11.4	1.38	1.00
Minor error	-12.1	9.8	9.2	13.4	1.07	1.06
Tritan error	-80.8	16.3	6.4	17.5	2.07	1.77
Congenital CVD:
Protanope	9.7	38.9	6.4	39.4	6.12	4.21
Deuteranope	-8.8	35.6	7.4	36.4	4.82	3.86
Tritanope	-86.8	28.2	6.0	28.8	4.74	3.06
Deuteranomal	-8.7	20.5	12.2	23.9	1.68	2.22
Acquired color vision loss:
DIDMOAD	81.7	27.7	25.4	37.6	1.09	3.00

Following are the guidelines for interpreting the Vingrys  and King-Smith data used in this article:

• Angle: The confusion angle identifies the type of color deficiency. According to Vingrys and King-Smith, an angle +3.0 and +17.0 indicates protanopia, a deuteranopia angles range between -4.0 and -11, while tritan have an angle greater than -70. Colblindor expands the ranges: protan defect begins at +0.7, from +0.7 to -65 is a deutan defect, and below -65 is a tritan defect.
• Major and minor radius: Vingrys and King-Smith use the moments of inertia method to determine color difference vectors. The major and minor moments of inertia are converted to major and minor radii to preserve the same unit of measure as used for the angles. These values can be used to determine the severity of the defect.
• Total Error Score (TES): In math terms, TES is the root mean square of the sum of the major and minor radii. Scores have an approximate range of 11 to 40+, with higher values indicating greater severity.
• Selectivity Index (S-index): The S-Index is the ratio of the major and minor radii. Values less than 1.8 indicate normal vision, or random values.
• Confusion Index (C-Index): The C-Index the major radius of the subject and the minor radius for normal vision. The dividing line between normal and defective is 1.60.

A total of 12 tests were conducted. For these tests, the percentage of color blindness was 100%, as the MGWW and BVM studies only included those who were tested as normal, protanopia, deuteranopia, or tritanopia. For each type of color blindness, tests were conducted using a gamma of 1.0 and 1.2 (for Android, 1.2 is the equivalent of 2.2 in the original studies). For each gamma value, a separate test was conducted for the two different D15 RGB color ranges (D15A and D15B).

Three questions tested:

1. Does gamma make a difference?
2. Do D15A and D15B produce the same results?
3. Which simulation models pass the tests?

As we shall see, every model is different.

Test results for protanopia

Following are the Vingrys and King-Smith scores for the protanopia tests:

Table 2 - Protanopia test scores

D15	Gamma	Percent	Model	Angle	Major Radius	Minor Radius	TES	S-Index	C-Index
A	1.0	100	MGWW	12.8	43.5	17.0	46.7	2.55	4.71
A	1.0	100	BVM	3.4	36.6	13.3	38.9	2.76	3.96
A	1.0	100	MOF	0.2	35.6	13.0	37.9	2.74	3.85
A	1.0	100	Linear	2.4	35.4	10.1	36.8	3.52	3.83
A	1.2	100	MGWW	11.6	42.1	17.1	45.5	2.46	4.56
A	1.2	100	BVM	8.3	35.6	10.8	37.2	3.29	3.86
A	1.2	100	MOF	8.6	31.6	16.3	35.6	1.94	3.42
A	1.2	100	Linear	2.1	31.0	13.7	33.9	2.26	3.35
B	1.0	100	MGWW	13.0	42.2	17.2	45.6	2.46	4.57
B	1.0	100	BVM	1.5	33.8	12.7	36.2	2.66	3.67
B	1.0	100	MOF	12.6	40.4	12.8	42.4	3.17	4.38
B	1.0	100	Linear	9.6	34.7	14.4	37.6	2.42	3.76
B	1.2	100	MGWW	6.7	44.0	17.2	47.2	2.55	4.76
B	1.2	100	BVM	-12.6	31.9	13.4	34.6	2.39	3.46
B	1.2	100	MOF	5.7	31.3	12.7	33.8	2.47	3.39
B	1.2	100	Linear	7.8	31.5	14.4	34.7	2.20	3.41

Following are a few notes regarding the above scores:

1. MOF, for D15B and a gamma of 1.0, and MGWW, in all tests,  had high (40+) TES values, which indicate a strong protan defect. In all other test cases, the TES indicated a lesser degree of severity. The C-Index reflects the TES.
2. For D15A and a gamma of 1.0, the BVM, MOF, and Linear models returned results that were consistent with deuteranomaly and not protanopia. For D15A, the angles show that gamma does make a difference for BVM and MOF. These models return the correct results when using the CRT settings for a dim light background environment (gamma 1.2). However, the D15B results show BVM sliding from deuteranomaly to deuteranopia with a gamma change. The wrong answer in both tests.
3. The linear model returns values closer to deuteranomaly than to protanopia.
4. Neither gamma nor RGB colors make a difference to MGWW.

The following D15A diagrams confirm the above data.

Figure 1 - D15A Gamma 1.0 Protanopia

These diagrams illustrate that  each model creates a unique color wheel. The resulting color wheel is not like turning a dial, but has transitions. It is the transitions that create confusion.

In Figure 1, MGWW illustrates a classical diagram for protanopia due to the number of lines that are parallel to to the dashed protan line. While BVM and MOF have low angles, they have lines that are parallel, or nearly parallel, to the protan lane. The linear model, on the other hand, has clear deutan lines.

As shown in Figure 2, gamma has a variable impact.

Figure 2 - D15A Gamma 1.2 Protanopia

While the angle is slightly smaller in Figure 2, MGWW still provides a clear definition of protanopia. Although the angles are in the protan range, the graphs for BVM and MOF show clear deutan lines. Again, the Linear model leans towards deuteranomaly.

The problem with converting the Munsell color system to RGB resulted in two sets of RGB values for the Farnsworth D15 test. The graphs in Figure 3 and those in Figure 1 illustrate the difference with a gamma of 1.0.

Figure 3 - D15B Gamma 1.0 Protanopia

In Figure 3, MGWW remains essentially the same as Figure 1. BVM shows both protan and deutan lines, which results in a low angle leaning towards deuteranomaly. Both the MOF and Linear models indicate protanopia.

Figure 4 has an interesting twist.

Figure 4 - D15B Gamma 1.2 Protanopia

Changing colors does not impact on MGWW. With no clear protan lines, BVM went to deuteranopia. MOF has both protan and deutan lines, but scores as protan. The Linear model scores as protan with D15B colors.

Test results for deuteranopia

For deuteranopia, most angles move from positive to negative as shown in Table 3.

Table 3 - Deuteranopia test scores

D15	Gamma	Percent	Model	Angle	Major Radius	Minor Radius	TES	S-Index	C-Index
A	1.0	100	MGWW	-10.2	38.2	20.3	43.2	1.88	4.13
A	1.0	100	BVM	-6.5	30.2	14.7	33.6	2.06	3.27
A	1.0	100	MOF	-21.4	28.2	15.8	32.3	1.79	3.05
A	1.0	100	Linear	-4.5	37.3	18.9	41.8	1.97	4.04
A	1.2	100	MGWW	-10.2	38.2	20.3	43.2	1.88	4.13
A	1.2	100	BVM	2.7	34.8	17.3	38.9	2.01	3.77
A	1.2	100	MOF	4.1	25.8	13.0	28.8	1.99	2.79
A	1.2	100	Linear	-14.8	29.9	15.3	33.6	1.95	3.24
B	1.0	100	MGWW	-7.9	38.0	20.1	43.0	1.89	4.12
B	1.0	100	BVM	-8.6	34.0	16.5	37.8	2.06	3.68
B	1.0	100	MOF	-9.5	34.7	14.5	37.6	2.39	3.75
B	1.0	100	Linear	6.3	36.4	13.2	38.8	2.75	3.95
B	1.2	100	MGWW	-7.9	38.0	20.1	43.0	1.89	4.12
B	1.2	100	BVM	-17.5	31.7	14.7	35.0	2.15	3.43
B	1.2	100	MOF	-10.9	23.5	13.5	27.1	1.74	2.54
B	1.2	100	Linear	-6.8	31.0	17.4	35.5	1.78	3.35

Notes regarding deuteranopia test scores:

1. For MGWW, the angles change somewhat between D15A and D15B, but the S-Index and C-Index change very little. MGWW remains the most consistent model.
2.  BVM only returns deuteranopia scores with D15B, while scoring as deuteranomaly with D15A.
3. Twice the S-Index for MOF moves to the normal/random range. The only correct score for MOS is D15B at gamma 1.0.
4. The Linear models returns two scores in the deuteranomaly range, and one score as protanopia. Only D15A at a gamma 1.2 returned a deuteranopia score.

 The drawings will help clarify what is happening with the BVM, MOF and Linear models.

Figure 5 - D15A Gamma 1.0 Deuteranopia

In Figure 5, MGWW represents a standard deuteranopia pattern. The BVM and Linear models are better representations of deuteranomaly than deuteranopia. The low S-Index raises questions about the MOF model, but it does have one deutan line, which makes it a mild case of deuteranomaly.

Figure 6 - D15A Gamma 1.2 Deuteranopia

As shown in Figure 6, changing the gamma had very little impact on MGWW. BVM has both protan and deutan lines. For BVM, a gamma of 1.2 accentuated the deuteranomaly. The graph for the MOF model explains the low S-Index and low C-index. MOF represents low deuteranomaly, and not deuteranopia. Increasing the gamma made the scores worse for MOF. The Linear model actually benefitted from the increased gamma, with more lines aligned with the deutan axis.

Figure 7 - D15B Gamma 1.0 Deuteranopia

As shown in Figure 7, MGWW exhibited a minor change from D15A to D15B, but the graph is still that of a deuteranope. The BVM and MOF models both produced better deutan lines, as express in the angles. Meanwhile, the Linear model became a protan. Does changing the gamma to 1.2 make a difference?

Figure 8 - D15B Gamma 1.2 Deuteranopia

In Figure 8, MGWW produced the same results as Figure 7. BVM and MOF both have deutan lines that justify their deuteranopia score. The Linear models still has both deutan and protan lines, but scores as a deuteranomaly with a gamma of 1.2.

Test results for tritanopia

Tritanopia raises serious questions regarding model behavior as shown in Table 4.

Table 4 - Tritanopia test scores

D15	Gamma	Percent	Model	Angle	Major Radius	Minor Radius	TES	S-Index	C-Index
A	1.0	100	MGWW	-80.0	30.7	14.2	33.9	2.16	3.33
A	1.0	100	BVM	-80.1	27.1	15.2	31.1	1.78	2.93
A	1.0	100	MOF	62.0	9.2	6.7	11.4	1.38	1.00
A	1.0	100	Linear	-87.2	28.2	12.9	31.0	2.19	3.05
A	1.2	100	MGWW	-85.5	27.6	15.8	31.8	1.75	2.79
A	1.2	100	BVM	-85.7	25.2	18.8	31.4	1.34	2.73
A	1.2	100	MOF	62.0	9.2	6.7	11.4	1.38	1.00
A	1.2	100	Linear	-87.7	28.6	15.5	32.5	1.84	3.10
B	1.0	100	MGWW	-87.2	28.1	14.9	31.8	1.88	3.04
B	1.0	100	BVM	-75.5	20.8	11.9	23.9	1.75	2.25
B	1.0	100	MOF	62.0	9.2	6.7	11.4	1.38	1.00
B	1.0	100	Linear	-81.0	27.2	13.8	30.5	1.97	2.94
B	1.2	100	MGWW	-87.1	27.8	14.9	31.6	1.87	3.01
B	1.2	100	BVM	-82.8	30.5	14.4	33.8	2.12	3.31
B	1.2	100	MOF	62.0	9.2	6.7	11.4	1.38	1.00
B	1.2	100	Linear	-78.6	35.0	11.3	36.8	3.1	3.79

Notes on Table 4:

1. Only MGWW model passed the tritanopia tests.
2. MOF tested as a normal with a rotated color wheel.
3. The BVM model tested closer to tritanomaly than tritanopia. For BVM,the S-Index was below 1.80 in 3 out of the four tests.
4. The Linear model actually scores better than BVM for tritanopia.

The charts should confirm the above model behavior.

Figure 9 - D15A Gamma 1.0 Tritanopia

In Figure 9, MOF tests as normal, as there are no confusion lines. MGWW is similar to the tritanopia graph shown in Vingrys and King-Smith paper, while the Linear model is similar to the graph in the Richmond Products scoring instructions. The BVM model is hard to interpret, as the there are only a few lines that are at angle to the tritan line.

Figure 10 - D15A Gamma 1.2 Tritanopia

In Figure 10, MGWW has a minor transition, but still scores as tritanopia. MOF scores as normal. With a gamma of 1.2, the BVM graph has more tritan lines, but still looks more like tritanomaly. The increased gamma did not help the Linear model, as it is beginning to look more like tritanomaly than tritanopia.

Figure 11 - D15B Gamma 1.0 Tritanopia

Although it is hard to see in Figure 11, there is actually a line between 10 and 11 for MGWW. Changing colors did create another minor transition, but MGWW still tests as tritanopia. MOF is still a color shifted normal. The BVM and Linear models reflect tritanomaly and not tritanopia.

Figure 12 - D15B Gamma 1.2 Tritanopia

In Figure 12, MGWW still tests as tritanopia, and MOF as normal. A gamma of 1.2 definitely helped the BVM model to look more like tritanopia. The change in gamma, resulted in the Linear model appearing as tritanomaly and not tritanopia.

Analysis of test results

This test of simulation models was limited to three questions. The answers to these questions raise further questions that become the subject of future tests.

Do the RGB colors alter the test results?

As mentioned above, there are two sets of colors used for the Web version of the D15 Panel. These two sets of RGB colors are referred to as D15A and D15B. Holding the gamma constant, and just looking at the tests based on RGB colors, there are differences. However, the changes were not consistent. The change could be radical such as the gamma 1.2 protanopia test for BVM. BVM tested positive for protanopia under D15A, but returned a deuteranopia result for D15B. For the deuteranopia test the reverse was true. BVM changed from protanopia inder D15A to deuteranopia under D15B.

Is the problem the model or the RGB colors? If you look at the scores for MGWW, the scores varied according to the RGB color, but the results produced the same diagnosis. As mentioned above, the Munsell color caps hold the saturation and value to 6, and only vary the hue. Since the RGB color system does not consider chromaticity or luminosity, RGB colors have to be converted to HSV to determine the hue. The resulting HSV values do not have a constant saturation and value. The same holds true when converting RGB to HSL. The variations in saturation and value introduce minor variation in the test results. Radical variations indicate problems within the model, itself.

Does gamma make a difference?

With the exception of the D15B protanopia test, gamma has very little impact on the MGWW scores. In all cases, MGWW passed the tests. This is not the case for the BVM, MOF, and Linear models. Unlike human subjects, the parameters are known. The question is whether the output of the model diagnosis the condition provided to the model. In the case of gamma, neither a gamma of 1.0 or 1.2 consistently results in passage of a test.

Using BVM as an example:

• For D15A, a gamma of 1.2 returns better results for protanopia, and poorer results for deuteranopia. 
• For D15B, the reverse is true.

For a given RGB color set, a model should behave consistently for all types of CVD.

Which model returns the best results?

There is only one model that consistently returned the correct result for every test, and it is MGWW (Meyer-Greenberg-Wolfmaier-Wickline). Every other model returned mixed results.

BVM (Brettel-Vienot-Mollon) has a problem differentiating between between protanopia and deuteranopia. Even though all tests were for 100% color blindness, BVM returned results consistent with anomalous trichromacy. 

Both the MOF (Machado-Oliveira-Fernandes) and Linear models are pre-calculated models. While such models offer higher performance, the performance comes at the cost of accuracy. With the exception of trichromacy, MOF returns slightly better results than the Linear model.

Conclusions

These tests highlighted several issues:

• The different results between D15A and D15B raises questions about thee RGB colors used in digital testing. A color corrected monitor won't resolve these differences. To advance research, a standardized set of RGB colors is needed for the Farnsworth-Munsell 100 Hue test and the Farnsworth D15 Panel.
• For the Farnsworth D15 Panel, a colorblind simulator should produce results that approximate those of humans who have taken the test. A review of the data provided in this article reveals that the BVM, MOF and Linear models often fail to meet this criteria. A simulation model must simulate human responses.

The results produced by these tests are educational, in that they:

• Emphasis that each person has a color wheel. Both the FM 100 and D15 tests are color wheels.
• CVD is not just a rotation of the color wheel, the order of the colors is altered.
• CVD is about the inability to distinguish colors. We do not know the color seen by any person.

The following images are for each of the models tested with a gamma of 1.0. Each image is a concatenation of the normal, protan, deutan, and tritan images. What do these images tell us about the validity of each model?

Figure 13 - Brettel-Vienot-Mollon at gamma 1.0

Figure 14 - Linear at gamma 1.0 

Figure 15 - Machado-Oliveira-Fernandez at gamma 1.0

Figure 16 - Meyer-Greenberg-Wolfmaier-Wickline at gamma 1.0

Nothing!
Images emphasis color, which is an illusion.
Images hide the transitions that cause confusion.
Images are useless when selecting text colors.